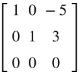Introduction to Reduced Row Echelon Form - Complete guide to RREF

Method of linear equations may be solved by lowering its augmented matrix to some Reduced Echelon Form (REF), which reproduces the identity matrix.

Echelon form can be considered as a series of elementary row operations performed on the associated augmented matrix obtained from the system of equations. The operations are:

1) Interchange one row with another row of the matrix

2) Multiply a row of the matrix by some non-zero constant

3) Replace the one row with the one row plus a constant times another row of the matrix.

The reduced row echelon form (RREF) technique can be used to solve the system of equations. Using the RREF method, the coefficients and constants are put in one matrix (called the augmented matrix or coefficient form). After defining the augmented matrix, a sequence of row-wise operations are done to change the augmented matrix into a form called RREF.

A matrix is said to be RREF if following conditions are met:

a) A row having zero at its every element, then such row should lie below any other row (that contains a non-zero element).

b) The left-most non-zero element of a row is 1

c) The left-most non-zero element of a row is the only non-zero element in its column.

d) Consider any two different left-most non-zero elements, let one is located in the i^th row and j^th column and the other is located in row “s” and column “t”. If , then .

Remember that a row having its all elements as zero is called a zero row and the left-most non-zero element of a non-zero row is a leading 1. A pivot column is one that contains a leading 1. The number of non-zeros rows should be equal to the number of pivot columns and the number of leading 1's.

Example:

Consider the matrix 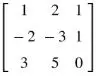. Let us do row operations on the matrix to convert it into reduced row echelon form.

Operation 1: Multiplying Row-1 by 2 and adding the resultant (new) row to Row-2. The New matrix will be

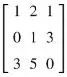
Note that Row-1 and Row-3 are same as original matrix, it is because we have not performed any operation on them.

Operation 2: Multiplying Row-1 by and adding it to Row-3. The new matrix will be

Operation 3: Multiplying Row-2 by 1 and adding it to Row-3, the matrix will be

Note that at this step the matrix is in REF. However, Multiplying Row-2 by and adding it to Row-1, the matrix will be converted to RREF.

That is